What is constitutive modeling?

In the physical phenomena we witness, conservation laws of physical quantities (governing equations) such as momentum, mass, and energy are satisfied.
In order to predict a phenomenon, the governing equations must be solved, which requires an equation (model) that represents the properties of the material.
To solve the equation of equilibrium of an object, a constitutive model representing the change in stress is required.
In general geotechnical engineering and soil mechanics, this corresponds to the stress-strain equation or the Darcy law that relates the flow rate to the total water head.

Geotechnical materials include sand, clay, gravel, soft rock, and hard rock, and they are formed by various processes such as sedimentation and alteration.
In addition to water and air, microorganisms also exist in the ground. Various substances and ions are dissolved in groundwater.
In such ground, load changes due to construction and seismic motions, water pressure changes due to groundwater infiltration from heavy rainfall, and water pressure changes due to drying, wetting, and freezing are all factors that contribute to the formation of the ground.
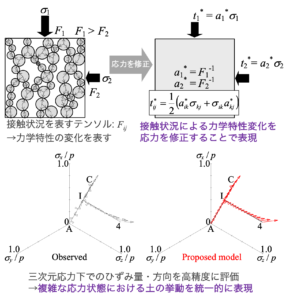
Groundwater content and phase changes due to drying, wetting, and freezing, and mineralogical changes due to ionic discharge and inflow, etc. can occur. (Figure 1)
In order to predict and represent these phenomena, governing equations and material models appropriate to the phenomena are required and solved.

To establish a model, it is necessary to
1. To find the relationship governing the phenomenon
2. To propose a physically and mathematically reasonable model (theoretical equation)
3. To verify the validity of the model.
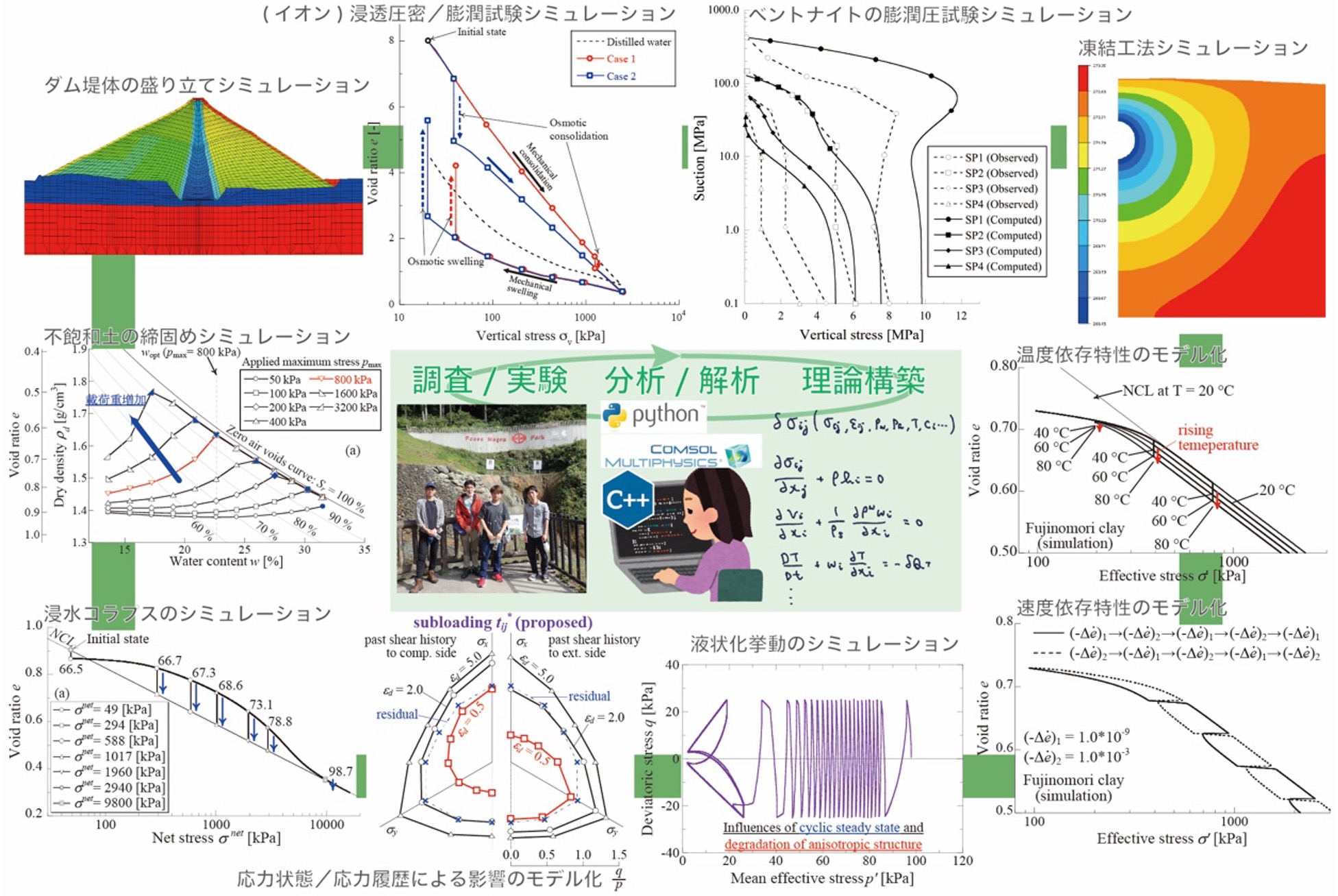
(In our laboratory, we conduct elemental tests and chemical analysis to investigate the phenomena for the above point 1. Regarding point 2, we formulate the theoretical model referring to knowledge in elastoplasticity, interface science, and so on. Regarding point 3, we develop an in-house program and utilize commercial software. (Figure 2)